勾股定理是几何中一条非常重要的定理,如果少了它,几何中几乎所有关于长度的计算公式都将失效,我们再也无法通过两点的坐标计算它们之间的距离,无法计算一条曲线的长度,无法知道圆的方程是二次曲线,它还间接地影响三角函数和复数等众多领域,可以说如果没有勾股定理,数学中大部分的内容将不得不被砍掉。
勾股定理的证明有很多种,其中有一些证法很麻烦,有一些较简洁,我国的商高、赵爽和古希腊的欧几里德都是在直角三角形的三边上各画一个正方形,然后用割补法证明直角边的两个三角形面积之和等于斜边上的三角形面积。近现代出现了很多简化的证明,其中有很多以面积为工具,有些已相似形理论为工具,等等。近年来又出现了利用微积分方法的证明,但它们都没有逃脱几何的影子,在证明中都是直接地考察一个直角三角形的几何图形。
关于代数与几何的关系,初中生有时候在做零星的几何题时会有所体会,比如,用方程的方式求解一条线段的长度,或求解一个角,或证明两个值之间的关系,等等。这些代数的零散应用依然没有逃出几何的框架。
代数第一次大规模进军几何领域应该是笛卡尔的解析几何。有了平面或空间上的坐标系,每一个点都有了一个坐标,使用两个或三个数组成的数组就可以表示一个点,几何的问题就通过坐标转换成了代数中的方程或计算的问题。不管多么困难的几何问题,通过转换,原则上都是可以用代数方法解决的。
不过,勾股定理在这个过程中起到了一个更加基础的作用,坐标系中两点之间的距离公式就是由勾股定理得出的,因此无法在解析几何中用这个公式再证明勾股定理了。
可见,在高中的解析几何中,虽然代数方法已经可以在几何领域大显身手,但几何还是占据了十分重要的基础地位。
真正将几何代数化,我认为是在向量被引入数学之后。从此,代数思想占据了几何中更加基础的位置。从勾股定理的向量证法中可以很深地体会这一点。
记向量u和v的内积为<u,v>,表示u向v投影的长度与v长度的乘积,再根据投影后的u和v是同向还是异向取正号或负号。
显然u,v垂直时 <u,v>=<v,u>=0,
并且可以很容易地证明<u+v,w>=<u,w>+<v,w>,<u,v+w>=<u,v>+<u,w>,
还有,一个向量的长度的平方就是它和它自己的内积:||u||²=<u,u>。
有了这些简单得近乎显然的性质,就可以轻松地推出勾股定理:
设直角三角形两边对应向量分别为u,v,那么斜边的长度就等于||u+v||,那么
||u+v||²=<u+v,u+v>=<u,u+v>+<v,u+v>=<u,u>+<u,v>+<v,u>+<v,v>。
因为<u,u>=||u||²,<v,v>=||v||²,<u,v>=<v,u>=0,故得勾股定理:
当u,v两向量互相垂直时,||u+v||²=||u||²+||v||²。
我相信有一些人在第一次见到这个证明的时候,都和我一样地感到惊奇,没有画任何图形,甚至没有考虑图形上的任何细节和特征,轻描淡写地几步运算,竟然就这么容易地推出了几何中一条基本定理!它像魔法师的兔子一样跳到你面前,你即使知道了证明的过程,还是不理解它究竟是为什么可以这么证明。你期望看到魔术师帽子里的秘密,或者,也许你能发现下面隐藏着循环论证的错误也说不定呢,就像用解析几何证明勾股定理一样的错误。
也许,把它原原本本地还原为一个几何的证明会对我们的理解有帮助,看看在这奇迹的背后究竟发生了怎样的过程。
第一步,||u+v||²=<u+v,u+v>,这步没什么可说的。
第二步,<u+v,u+v>=<u,u+v>+<v,u+v>,
这步应用了内积的线性性质,是关键的一步。在图形上跟踪一下这个过程: 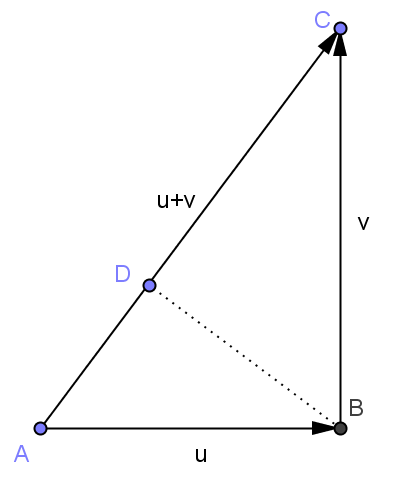
我们在一个直角三角形中画出斜边上的高,将u+v向自己的投影分解成u向u+v的投影和v到u+v的投影之和,在图中u和v向斜边(u+v)的投影分别是直角三角形斜边上的顶点到垂足和垂足到另一顶点的向量,即AD和DC。把这一步还原成几何的语言就是AC²=AC*(AD+CD)。
第三步,<u,u+v>=<u,u>+<u,v>=<u,u>=||u||²,和<v,u+v>=<v,u>+<v,v>=<v,v>=||v||²,
这一步中有意思的是这里,<u,u+v>既可以看成u向u+v投影之后再与u+v乘积,也可以看成u+v到u的投影与u的乘积,即u的长度平方,因此这步翻译成几何的语言就是AB²=AD*AC。同样地有<v,u+v>=||v||²等价于BC²=AC*DC。而这正是初中生都熟知的射影定理。
由AC²=AC*(AD+CD)和AB²=AD*AC、BC²=AC*DC立即可以得到勾股定理。
至此,它背后的秘密算是完全揭开了:内积的实质就是投影,内积是线性的,是因为投影映射是线性的,内积的交换律也是由投影下形成的相似三角形性质决定的,它的特例就是射影定理,因此,用内积证明勾股定理,其实质就是用射影定理证明勾股定理。
但是,我还是觉得很神奇,因为在用向量分析的时候,我们只是在计算,虽然它实质上是射影定理,但在用向量内积推导的过程中我丝毫没有觉察出它跟几何有什么联系,与绞尽脑汁的几何证明题相比,我似乎在不知不觉中就被带到了真理的地方。可见,用向量方法分析和直接用射影定理证明勾股定理,其思维方式上是有很大差别的。这就是代数思维和几何思维的不同之处。
为了使直线上的几何问题代数化,人们引入正数和负数,为了使平面和空间的几何问题代数化,人们引入坐标系,这些都内在蕴含了向量的思想,但是都没有明确地把向量的概念提出来。随着经典力学的发展,随着人们对力、加速度、速度和位移这些概念之间关系的深入研究,矢量这个概念逐渐被人们认识并加以抽象概括,形成了向量代数。用向量描述世界,比以前的数和几何对象有更高的概括性和统一性,现在,以向量空间和它们之间的变换为主要研究对象的线性代数已经在各个应用领域中发挥着无法替代的作用。
我们再看一下在物理的能量守恒观点下的勾股定理。设想你把一个石块从手中斜抛出去,石块初始速度为v0,v0可以分解为水平速度v1和竖直速度v2,按照向量的写法,有\( v_0=v_1+v_2\)。石块的初始动能为\( \frac{1}{2}mv_0^2\),经过一段时间,石块竖直方向的速度变为零,只剩下水平速度v1,这时它的动能为\( \frac{1}{2}mv_1^2\),因此有\( \frac{1}{2}m(v_0^2-v_1^2)\)的动能减少,而势能增加量恰好是\( mgh=\frac{1}{2}mv_2^2\),注意它们之间的关系,当且仅当\( v_0^2=v_1^2+v_2^2\)时,总的机械能是守恒的。也许,上帝在创造世界的时候,为了能让他的能量守恒原则成立,不得不承认勾股定理,或者反过来,因为要创造一个满足勾股定理的世界而使这个世界上的能量守恒。
想一想在这个过程中是什么发挥了主要作用,其中主要的决定性因素就是水平与竖直方向上的运动互不干扰,可以说两个方向无关,真实物体的运动是两个无关方向上运动的线性叠加,这样重力做功才跟路径无关,机械能守恒。
可以说世界上有很多问题,看似很复杂,但实际上可以分解成一些彼此无关的因素的线性叠加。利用这个特性,当考虑整体比较麻烦时可以把它分解,分而治之,然后再回到整体;而当分析众多错综复杂的分量有困难时也可以先从整体入手。而向量恰好是整体与分量的对立统一,这就是向量代数的力量源泉。
4月27日有关余弦定理的补充:
评论中有人说这个证明中用到了一些内积的性质是依赖于余弦定理的,而余弦定理又是来源于勾股定理,因此还是循环论证了。
我的观点在下面评论答复中已经说过了,内积的那些性质(在文中列出的用来证明勾股定理的那些性质:实数欧几里得空间内积的交换律、双线性、垂直时内积是零)没有一条是必须依赖于余弦定理的。现在补充一点,即使不用那个”u,v垂直时<u,v>=0″逻辑上仍然讲得通。
利用双线性和交换性(这两条性质依赖于平行和相似),有余弦定理(因此,余弦定理本质上是内积的二次展开式,这也是为什么余弦定理和二次的牛顿二项展开式那么相似):
||u-v||²=<u-v,u-v>=<u,u>+<v,v>-<u,v>-<v,u>=||u||²+||v||²-2<u,v>
||u+v||²=<u+v,u+v>=<u,u>+<v,v>+<u,v>+<v,u>=||u||²+||v||²+2<u,v>
当u,v垂直时,利用矩形两对角线长度相等(此依赖于三角形全等),有||u+v||=||u-v||,则有
<u,v>=<v,u>=0,和勾股定理||u-v||²=||u+v||²=||u||²+||v||²
这倒是个一举多得的证法。