在本博客文章《理解矩阵与矩阵乘积(三)》六、矩阵分块的实质中,已经提到过矩阵分块乘法是有清晰的几何意义的。写那篇文章的时候我的头脑中还浮现出一个图表,为什么矩阵乘法和分块的乘法有一样的计算规则,在图表中一目了然。但当时嫌画图太麻烦没有画出来。几个月过去了,那篇文章的浏览量也不小,但似乎那篇文章说得还不够清楚。因此这里把当时想到的图表补充进来。
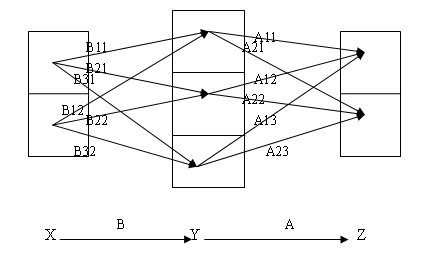
图示:2×3与3×2分块矩阵的乘法
设 \( X,Y\) 是两个向量空间,\( A,B\) 分别是 \( Y\) 到 \( Z\)、\( X\) 到 \( Y\) 的线性映射,它们两个的复合映射是从 \( X\) 到 \( Z\) 的,可以用两个矩阵的乘积 \( AB\) 来计算。
我们把 \( X\) 按照基底的顺序分成两个子空间(例如,设 X 是三维空间,x,y,z 是它的基底,将 xoy 平面和 z 轴作为 X 的两个子空间),把 \( Y\) 按照基底的顺序分成三个子空间,把 \( Z\) 按照基底的顺序分成两个子空间(\( Z\) 子空间个数不必与 \( X\) 子空间个数相等,它们都可以分成是三个,四个或其它数目的子空间。)在上面的图示中,我们用方格子代表分得的子空间,X 上方的两个方格代表 X 中的两个子空间。
这样,图中的箭头代表各个子空间之间由原来映射诱导出来的新的映射,比如,图中标明 B11 的箭头,表示 \( X\) 第一个子空间中的向量经过 \( B\) 的映射到 \( Y\) 中,又向 \( Y\) 的第一个子空间做投影得到的向量,考虑下面的与这种分解方式相对应的分块矩阵的乘法,这个映射的矩阵实际上就是 B11。
\( AB=\begin{pmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\end{pmatrix}\begin{pmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\\B_{31}&B_{32}\end{pmatrix}\)
\( =\begin{pmatrix}A_{11}B_{11}+A_{12}B_{21}+A_{13}B_{31}&A_{11}B_{12}+A_{12}B_{22}+A_{13}B_{32}\\A_{21}B_{11}+A_{22}B_{21}+A_{23}B_{31}&A_{21}B_{12}+A_{22}B_{22}+A_{23}B_{32}\end{pmatrix}\)
分块矩阵运算结果,第一行第一列矩阵块,是从 \( X\) 第一个子空间到 \( Z\) 第一个子空间的映射,等于 \(A_{11}B_{11}+A_{12}B_{21}+A_{13}B_{31}\),恰好是图中 \( X\) 第一个方格经由 \( Y\) 的三个方格到达 \( Z\) 的第一个方格的这些映射复合的叠加。
Pingback: 再谈矩阵与矩阵乘法 | 数学笔记