以前写了几篇相关的文章,见
《图示矩阵分块乘法》《理解矩阵与矩阵乘积(三)》《理解矩阵与矩阵乘积(二)》《理解矩阵与矩阵乘积(一)》
如果你从网上搜“理解矩阵”或“矩阵乘积”,还可以搜到孟岩写的系列文章《理解矩阵》以及很多其他作者写的文章。尽管经过很多人的努力,试图说清楚矩阵和矩阵的乘积的最本质的意义,这个问题似乎还在困扰着很多人。
我对矩阵和矩阵乘积的意义的认识,基本上在《图示矩阵分块乘法》中已经阐述,但之所以还要写这篇文章,是因为不论是我的文章,还是网络上其他相关文章,都没有做到把这个问题彻底讲清楚,我是学数学的,和很多其他学数学的人一样习惯上以数学抽象的概念去解释另一个概念,所以讲到矩阵总是会提向量空间,会提向量,但工科的学生往往是不会接触向量空间的概念,所以这种解释虽然我们看起来很直观,对工科的学生往往就很难理解了。还有一般的教材里都会讲到的从线性映射的复合的观点去定义矩阵的乘法,但仍然解释不清乘法规则的本质,尤其解释不了矩阵乘法为什么可以分块进行。
我博士的课题是研究随机矩阵,我的导师之一有无线通讯的背景,所以我有幸接触到一个能够更加直观阐释矩阵的概念和矩阵乘法规则的通讯模型,它虽然是个具体的模型,但我认为它有可能触及到了矩阵和矩阵乘法的最本质的东西。
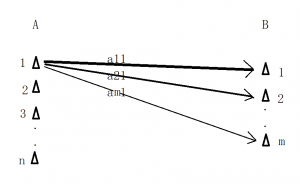
如图一,考虑在 A 地建有一个发射站,其中有 n 个发射塔,B 地一个接收站,有 m 个接受塔。他们之间要传递的是一组由n 个数组成的信息 (x1,x2,…,xn),这样,这组信息可以由这n个发射塔同时发出,然后m个接收塔会同时收到它们发送过来的数据。
但因为距离等因素的影响,每个发射塔发出的信息到不同的接收塔的过程中会有不同程度的衰减,比如第一个发射塔发出的信息x1到第一个接收塔就变成了 a11x1,等等,它们对应的关系可以列成一个方阵:
接收B\ 发射A 1 2 3 …… n
1 a11 a12 a13 a1n
2 a21 a22 a23 a2n
… ….. …. …. ….
m am1 am2 am3 ann
这个对应关系的表格其实就是我们的矩阵了。有人可能觉得这只是形式上的对应关系,这些元素只是形式上构成了一个矩阵的形状,和我们数学上的矩阵有什么关系呢?矩阵的乘法在哪里呢?其实关系大得很。考虑一下发射站每发射一条信息 (x1,x2,…,xn),那么在接收站接收到的信息会是什么样子?比如第一个接收塔接到的是所有发射塔给它发的信息,那就是 y1=a11x1+a12x2+…+a1nxn,同理第二个接收塔收到的是 y2=a21x1+a22x2+…+a2nxn,等等。
如果凭直观感觉,如果很多发射塔同时发射信息,所有的接收塔收到的都是这些信息相互混杂的结果,似乎接收端很难分辨还原出原始的信息,就像一群人同时向另一群人喊话,每个人听到的只有混在一起的噪声,根本听不清谁到底说了什么,但是从数学上分析一下会发现,只要接收塔不比发射塔少,只要这个方阵的性质足够好,接收端就可以综合所有接收到的信息并计算还原出原始信息,这就是对线性方程组的研究得出的结论。
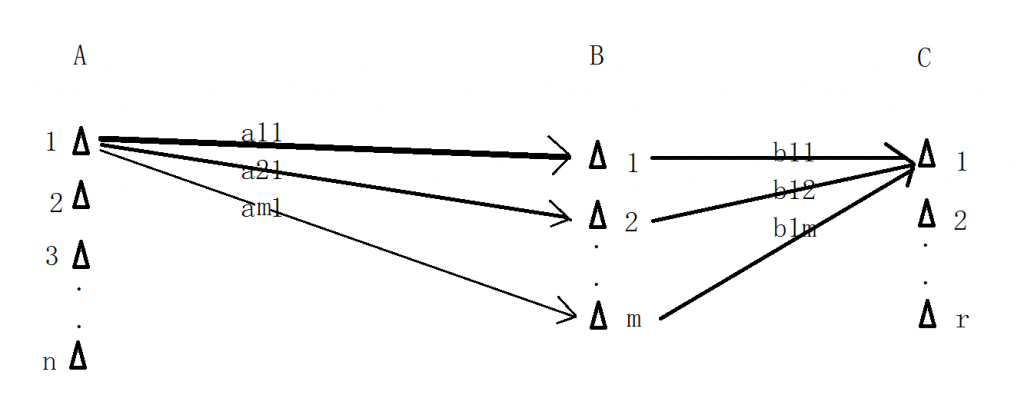
接下来考虑,如果B只是个中转站,它也要把它接受到的所有信息原封不动地传给C,那就是下图这样:
那么C最后接到的信息会是什么样?如果像刚才那样分析从B到C的过程,那C接到的信息就是 z1=b11y1+b12y2+…+b1mym; z2=b21y1+…+b2mym,等等。但是,我现在想把B这个中转站从图中隐去,我想直接制定一个从A到C的发射-接收转换列表,我应该怎么制定呢?怎样才能把下面这个列表填完整呢?
接收C\ 发射A 1 2 3 …… n
1 ?
2
…
r
根据这个表中元素的定义,第一行第一列的元素(记为c11)应该是最原始的信息中的第一个元素 x1 被发射到最终位置C的第一个接收塔的过程中的衰减系数,而从图中不难看出,这个信息元 x1 首先经过一次衰减到达B的m个中转塔,也就有了 m 个分身a11x1, a21x1,…,am1x1,然后这m个分身又分别经过第二次衰减,并集合到C的第一个接收塔那里,于是变成了 a11b11x1+a21b12x1+…+am1b1mx1,那么自然就有
c11=a11b11+a21b12+…+am1b1m。
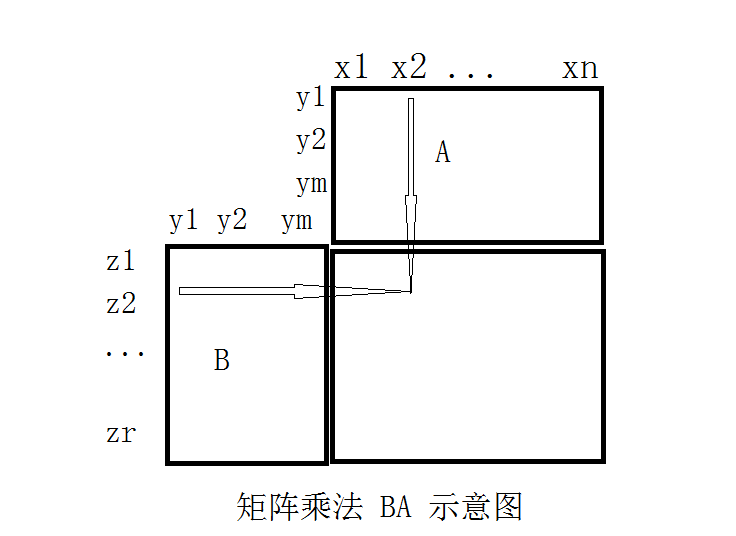
同理,A的第 i 个发射塔发出的信息要经过 B 的所有中转塔才能最终到达C处的第 j 个接收塔,这就是乘法矩阵中的 cij 要这样定义的原因。对应下面这个矩阵乘法BA的示意图:发射数据 xi 与矩阵 A 的第i列元素相乘之后到达 B 的 m 个中转塔,得到 yk=akixi,然后中转塔的这 m 个数据又分别和矩阵 B 的第 j 行元素乘积,并在 C 的第 j 个塔那里整合起来,于是就有了 cij 的又乘又加的表达式。
这个模型里的通信模型只是用来帮助理解和想象,现实生活中有很多模型都可以体现这样的运算关系,比如把通信站换成物流公司,把信息换成货物,矩阵的元素换成路程或运输成本,这就变成了一个物流模型;把信息换成空间中的向量,每个通信塔换成空间的基底,这就能解释空间中的线性映射,等等。
下面接着用通信模型解释矩阵的分块运算。首先理解什么是矩阵的一个子块:让我们先回到(图一)的没有中转站而只有发射和接收站的情形,然后考虑,原有的系统支持n个信息同时发射,但假设我现在要发射的信息没有那么多,只有 m(<n) 个分量,那么我可以只用其中的m 个发射塔;同时因为发射的数据减少了,也就不需要那么多接收塔了,所以我可以把其中的一些发射塔和接收塔关闭。假设剩下的塔之间传递信息的转换关系不变,那么剩下的那些塔就是原来的一个子系统。因为有些塔不工作,所以我也无需考虑跟它们相关的衰减系数,我们把原来矩阵中所有和关闭的塔相关联的行或列都去掉,剩下的矩阵就是这个子系统对应的衰减系数矩阵。
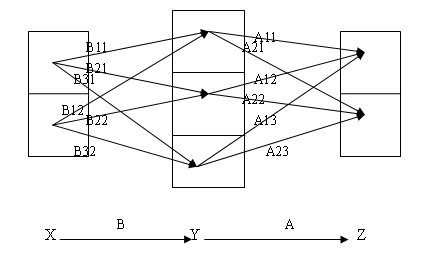
这样就好解释了为什么矩阵分块的乘法也具有同样的运算法则:还是考虑(图二)描述的发射-中转-接收模型,但我们这次以不同的眼光看:我们把发射、中转和接收塔都分别编组,把一组通信塔看成一个整体,那么一个发射组+一个中转组+一个接收组就构成了一个子系统,它们中间的衰减矩阵自然是大矩阵里的子块;而如果我们对这些子系统进行分析,它们之间的传递关系自然和把它们当成单个通信塔的情形是一模一样的:以下是我以前的文章《图示矩阵分块乘法》里贴过的图,想象每个方格里是一组通信塔,再结合那篇文章中论述的向量空间的模型,就不难理解其中的道理了。
最后多说几句我对线性代数中“线性”的认识。我们上面所有的分析,都是在我们所描述的系统可以分拆这个假设的基础上的,也就是上面所说,假定它的任何一个子系统的运行状态不受系统其它部分的干扰,只有这样,我们才能把输入的原始信息分成若干分量,它们通过系统传递之后再进行整合;也只有这样,我们把系统进行分拆,分别研究各个子系统之后再进行综合才是有意义的。所以,线性代数就是拆拆合合的技术,“线性”是我们进行拆拆合合的基础。