在本博客文章《理解矩阵与矩阵乘积（三）》六、矩阵分块的实质中，已经提到过矩阵分块乘法是有清晰的几何意义的。写那篇文章的时候我的头脑中还浮现出一个图表，为什么矩阵乘法和分块的乘法有一样的计算规则，在图表中一目了然。但当时嫌画图太麻烦没有画出来。几个月过去了，那篇文章的浏览量也不小，但似乎那篇文章说得还不够清楚。因此这里把当时想到的图表补充进来。
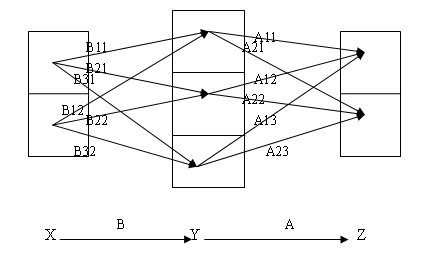
图示：2×3与3×2分块矩阵的乘法
Category Archives: 数学笔记
读书笔记。
点集拓扑要义（二）
（五）拓扑空间中的序列极限与集合聚点
极限是序列的极限，聚点是点集的聚点。但二者却有很大的联系，在欧氏空间或更一般的度量空间中，x 是一个点集的聚点，当且仅当在这个点集中可以取出一列收敛到 x 但每一项都不等于 x 的点列；如果 x 是一个序列的极限，并且这个序列中有无限多项不等于 x，那么 x 就是这个序列元素构成集合的聚点。
这一节试图充分讨论极限与聚点在一般的拓扑空间中的关系。
点集拓扑要义（一）
分析教材中有一部分是点集拓扑中的内容在欧氏空间中的应用，所以索性在温习的时候把点集拓扑也顺便复习一遍。当年我们用的是熊金城的《点集拓扑讲义》作为教材，所以现在还用这本书为底本做一些笔记性的补充。
隐函数定理的补充，隐函数可导性与可微性的讨论
定理1(隐函数定理)：设二元函数 \( F(x,y)\) 满足
i) \( F(x_0,y_0)=0\)
ii) \( F(x,y)\) 与 \( F_y(x,y)\) 在 \( (x_0,y_0)\) 的某个邻域内连续
iii) \( F_y(x_0,y_0)\not=0\)
则存在 \( \delta,\eta>0\) 和唯一的定义于 \( (x_0-\delta,x_0+\delta)\) 取值于 \( (y_0-\eta,y_0+\eta)\) 的函数 \( y=y(x)\) 满足
1) \( y_0=y(x_0)\)，\( F(x,y(x))=0,\forall xin(x_0-\delta,x_0+\delta)\)
2) \( y(x)\) 在 \( (x_0-\delta,x_0+\delta)\) 内连续
进一步地，如果
iv) \( F_x(x,y)\) 也在 \( (x_0,y_0)\) 的一个邻域内连续，则上述的 \( y=y(x)\) 在 \( x_0\) 的一个邻域内一阶导数连续，且
\[ y'(x)=-\frac{F_x(x,y(x))}{F_y(x,y(x))}\]
这就是南开大学《数学分析》（黄玉民，李成章 编）下册中隐函数定理的二元函数情形。而在某些教材上，只讨论了 \( F\) 在 \( (x_0,y_0)\) 的某个邻域内连续可微的情形，如张筑生版的《数学分析新讲》。
偏导数与可微性的进一步讨论
首先回顾一下多元函数的偏导数存在与可微的关系问题。
设 \( F(x,y)\) 是二元实函数，\( x_0,y_0\) 是其定义域的一个内点，如果存在两个实数 \( A,B\)，使得对于极限过程 \( \sqrt{h^2+k^2}\to 0\)，以下关系成立：
\( F(x_0+h,y_0+k)-F(x_0,y_0)=Ah+Bk+o(\sqrt{h^2+k^2})\)
则称 \( F\) 在点 \( (x_0,y_0)\) 处可微。
据《数学分析新讲》（张筑生著，北京大学出版社，1990）第二册209页叙述，一个多元函数可微的等价叙述为：
\( F(x_0+h,y_0+k)-F(x_0,y_0)=Ah+Bk+\alpha h+\beta k\)
其中 \( \alpha=\alpha(h,k), \beta=\beta(h,k)\) 满足
\[ \lim_{(h,k)\to(0,0)}\alpha(h,k)=\lim_{(h,k)\to(0,0)}\beta(h,k)=0\]
一个多元函数 \( F\) 在某点可微，意味着它在这点对各个变元的偏导数存在，但是偏导数存在却不蕴含可微性。如果函数 \( F\) 在某点的一个邻域中每个一阶偏导数都存在且这些偏导数都在该点连续，那么函数 \( F\) 在该点可微，但是 \( F\) 在某点可微却又不蕴含一阶偏导数在该点连续。
这些基本事实可参见任何一本数学分析教材。
各个教材只讨论所有一阶偏导数连续是可微的充分不必要条件，却没有讨论可以把这个条件减弱到什么程度依然可以蕴含可微的结论。那么我们是否可以把这个条件减弱呢？