注记部分:
1 命题 7.2 为何在实数空间不成立?
参见本博客文章《理解复数域上的向量空间(第一篇)》
2 \( U\) 是线性算子 \( T\) 的不变子空间,那么 \( T^*|_U=(T|_U)^*\) 是否成立?
在证明实空间自伴算子谱定理的时候,中间有一部,设 \( S=T|_{U^\perp}\) 然后验证 \( S\) 在 \( U^\perp\) 上也是自伴的。为什么这么验证呢?为什么不根据 \( T\) 是自伴的并且 \( U^\perp\) 是不变子空间这个事实,从而直接说 \( T|_{U^\perp}\) 是自伴的?
这涉及一个问题:如果 \( T\) 是一个一般的映射,\( U\) 是 \( T\) 的不变子空间,那么是否一定有 \( T^*|_U=(T|_U)^*\)?
这是不一定的,设
\( T=\begin{pmatrix}1&1\\ 0&1\end{pmatrix}\)
而 \( U=\{(x,0)\}\) 那么 \( U\) 是 \( T\) 的不变子空间。
那么 \( (T|_U)^*\) 是 \( U\) 上的单位变换,但 \( T^*|_U\) 却把 x 轴映射到了直线 y=x 上。\( U\) 不一定是 \( T^*\) 的不变子空间。
之所以出现这种情况,是因为在伴随的定义中,任意 \( w\),要求取 \( T^*w\) 是满足
\( \forall v, \langle Tv,w\rangle=\langle v,T^*w\rangle\)
的那个唯一的向量。
在 \( U\) 中的任意一个向量 \( w\),如果我们找到 \( (T|_U)^*w\in U\) 满足
\( \forall u\in U, \langle Tu,w\rangle=\langle u,(T|_U)^*w\rangle\)
上式中的 \( u\) 也只是限制在 \( U\) 中的,如果把 \( u\) 的范围扩大到整个空间中,那么上面的内积等式不一定成立。因此 \( (T|_U)^*\) 不一定等于 \( T^*|_U\)。
如果考虑 \( (T|_U)^*\) 和 \( T^*|_U\) 二者的关系,那么下面的事实是成立的:记 \( P_U\) 为到子空间 \( U\) 的正交投影,那么 \( (T|_U)^*=P_UT^*|_U\)。 证明也很容易。这样,\( (T|_U)^*=T^*|_U\) 能够成立的充要条件为 \( U\) 也是 \( T^*\) 的不变子空间。
3 实空间变换矩阵的分块上三角化与实空间的正规、自伴算子谱定理
如果实空间的分块上三角矩阵的相关内容放在第五章的位置,那么实空间的谱理论证明就变得跟复空间谱定理一样容易证明。它们不论从形式上还是从证明方法上都没有什么本质区别。
4 自伴算子乘积什么时候是自伴的?
问题:设 \( S\) 与 \( T\) 都是向量空间 \( V\) 上的自伴算子,那么 \( ST\) 和 \( TS\) 是自伴的吗?
由 \( (ST)^*=T^*S^*=TS\),如果 \( S\) 与 \( T\) 可交换,即 \( ST=TS\),那么有 \( (ST)^*=ST\) 和 \( (TS)^*=TS\),即两者都自伴。反过来若 \( ST\) 自伴,则 \( ST=TS\)。
但是 \( S\) 与 \( T\) 二者不一定是可交换的,反例如下:设
\( S=\begin{pmatrix}0&1\\ 1&0\end{pmatrix},T=\begin{pmatrix}1&0\\ 0&2\end{pmatrix}\)
那么
\( ST=\begin{pmatrix}0&2\\ 1&0\end{pmatrix}\not=\begin{pmatrix}0&1\\ 2&0\end{pmatrix}=TS\)
那么 \( S\) 与 \( T\) 满足什么条件时二者是可交换的呢?以下是一个充要条件:
命题1:设 \( S,T\) 是 \( V\) 上的线性变换,\( T\) 自伴,那么 \( ST=TS\) 当且仅当 \( T\) 的每个特征子空间 \( \mathrm{null}\,(T-\lambda I)\) 是 \( S\) 的不变子空间。
证明:如果 \( ST=TS\),那么 \( \forall v\in\mathrm{null}\,(T-\lambda I), (T-\lambda I)Sv=S(T-\lambda I)v=0\),这说明 \( Sv\in\mathrm{null}\,(T-\lambda I)\),因此 \( \mathrm{null}\,(T-\lambda I)\) 是 \( S\) 的不变子空间。
反过来,如果 \( T\) 的每个特征子空间都是 \( S\) 的不变子空间,那么在一个特征子空间 \( \mathrm{null}\,(T-\lambda I)\) 里的任意一个向量 \( v\),有 \( TSv=\lambda Sv=S(\lambda v)=STv\)。
再由自伴算子的谱定理,
\( V=\mathrm{null}\,(T-\lambda_1I)\oplus\mathrm{null}\,(T-\lambda_2I)\oplus\dots\oplus\mathrm{null}\,(T-\lambda_mI)\)
其中 \( \lambda_1,\lambda_2,\dots,\lambda_m\) 是 \( T\) 的全部特征值,可知任意向量 \( v\),有
\( \displaystyle TSv=\sum_{i=1}^mTSv_i=\sum_{i=1}^mSTv_i=STv\)
证毕。
备注:这个命题是从分析 \( S,T\) 的矩阵关系的过程中得到的,即设 \( T\) 在某正交基底下为对角形,分析另一个矩阵与这个对角矩阵可交换的条件,最后从元素满足的条件总结出这个命题。后来发现第五章习题已经讨论过这个问题的一半了。
5 正定算子的平方根
如果 \( \dim V>1\),那么单位变换 \( I\) 有无穷多个平方根。以二维空间为例,任意一个角度 \( \theta\),变换
\( \begin{pmatrix}\cos\theta&\sin\theta\\ \sin\theta&-\cos\theta\end{pmatrix}\)
都是单位变换的平方根。
如果把上面的变换写成复平面上的变换,那么 \( f(z)=\bar ze^{i\theta}\) 是复平面上单位变换的平方根,即 \( f(f(z))=1\)。它不是复数空间上的线性变换,但是如果把复数域看成实数线性空间,它是线性变换。
\( I\) 的上述形式的平方根都是自伴的,\( I\) 也有非自伴的平方根,比如,只要 \( a^2+bc=1\),那么
\( \begin{pmatrix}a&b\\ c&-a\end{pmatrix}^2=I\)
可见正定算子的平方根可以不是自伴的。
由此可知,一个正定算子,只要有一个特征值的重数超过1(即这个特征值的特征子空间超过一维),那么它有无数个平方根,其中也有无数个自伴的平方根。
如果一个二维空间上的正定算子有两个相异的特征值,那么在某正交基底下它的矩阵为
\( \begin{pmatrix}\lambda_1&0\\ 0&\lambda_2\end{pmatrix}\)
我们要找到它的所有平方根,即找到满足
\( \begin{pmatrix}a&b\\ c&d\end{pmatrix}^2=\begin{pmatrix}a^2+bc&b(a+d)\\ c(a+d)&d^2+bc\end{pmatrix}=\begin{pmatrix}\lambda_1&0\\ 0&\lambda_2\end{pmatrix}\)
的所有矩阵。
因为 \( \lambda_1\not=\lambda_2\),所以\( a^2\not=d^2\),故 \( a+d\not=0\),因此 \( b=c=0\),那么 \( a^2=\lambda_1, d^2=\lambda_2\),这个正定算子只有有限个(4个)平方根。
下面证明一般性结论:
命题2:如果一个 n 维空间上的正定算子 \( B\) 有 n 个相异的特征值,那么它只有有限个(\( 2^n\) 个)平方根,并且其平方根都是自伴的。
证明:如果 \( A^2=B\),那么 \( AB=A^3=BA\),即 \( A\) 与 \( B\) 可交换。因为 \( B\) 自伴,利用命题1,得 \( B\) 的每一个特征子空间(都是一维的)也是 \( A\) 的特征子空间,故可以选一组基底使得 \( A\) 与 \( B\) 的矩阵都是对角形,\( A\) 矩阵对角线上的元素就必须等于 \( B\) 矩阵对角线上相应的元素的平方根,这样的矩阵有 \( 2^n\) 个,且因为正数的平方根都是实数,所以这些矩阵都是实对称矩阵,因此 \( B\) 的平方根都是自伴的。
6 等距变换几个相似概念之间的关系
如果假定 \( T\) 是线性变换,那么以下条件是等价的:
1) \( T\) 是等距变换,即 \( \forall u,v\in V,\|Tu-Tv\|=\|u-v\|\)
2) \( T\) 保持范数,即 \( \forall u\in V,\|Tu\|=\|u\|\)
3) \( T\) 保持内积,即 \( \forall u,v\in V,\langle Tu,Tv\rangle=\langle u,v\rangle\)
但是如果 \( T\) 只是一个普通的变换,而没有线性变换的条件,这三个条件不是等价的。它们的推导关系如下图: 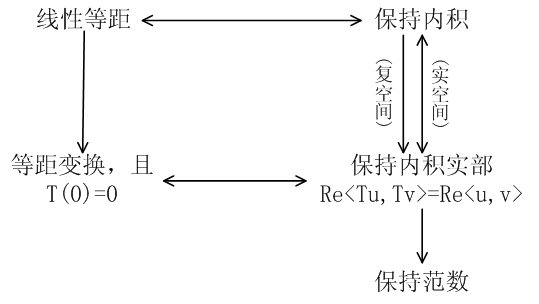
其中的箭头方向是必要条件的方向,双向箭头表示两个等价的命题,单项箭头表示两个命题不等价。下面分别证明如下:
线性等距变换保持内积,这个在书上已有证明;线性等距变换是把零向量映射成零向量的等距变换,这个也是显然的;保持内积的实部在实空间下和保持内积是一回事;因为内积诱导的范数只与内积的实部有关,即 \( \langle u,u\rangle\in\mathbf R\),所以保持内积实部的变换一定也是保持范数的。这些都是比较容易得出的结论,因此只需证明两个命题:保持内积的变换是线性等距变换;一个变换保持内积实部当且仅当它是将零向量映射为零向量的等距变换。
命题3:设 \( T\) 是向量空间 \( V\) 上的变换,如果任意两个向量 \( u,v\),有 \( \langle Tu,Tv\rangle=\langle u,v\rangle\),那么 \( T\) 是线性等距变换。
证明:因为 \( T\) 保持内积,所以它一定是保持范数的,那么只需证明 \( T\) 是线性变换,也就推出它是线性等距变换了。即只需证 \( T(u+v)=Tu+Tv\) 与 \( Tku=kTu\)。为此考察
\( \|Tku-kTu\|^2=\langle Tku,Tku\rangle-\bar k\langle Tku,Tu\rangle\)\( -k\langle Tu,Tku\rangle+k\bar k\langle Tu,Tu\rangle=0\)
其中最后一个等号成立是因为在每一个内积里可以把所有的 \( T\) 都去掉,最终得到0。因此 \( Tku=kTu\)。
同理考察 \( \|T(u+v)-Tu-Tv\|^2\),同样在打开的每一个内积中去掉 \( T\),最终为0。
因此 \( T\) 为线性映射。又因为 \( T\) 保持内积,所以由 \( \|Tv\|^2=\langle Tv,Tv\rangle=\langle v,v\rangle=\|v\|^2\),知 \( T\) 保持长度。由定义 \( T\) 是正交变换。
命题4:设 \( T\) 是向量空间 \( V\) 上的变换,那么 \( \forall u,v\in V,\mathrm{Re}\,\langle Tu,Tv\rangle=\mathrm{Re}\,\langle u,v\rangle\) 当且仅当 \( T\) 是等距变换,并且 \( T(0)=0\)。
证明:由于
\( \|Tu-Tv\|^2=\|Tu\|^2-2\mathrm{Re}\,\langle Tu,Tv\rangle+\|Tv\|^2\)
\( \|u-v\|^2=\|u\|^2-2\mathrm{Re}\,\langle u,v\rangle+\|v\|^2\)
如果 \( T\) 保持内积实部,那么 \( T\) 保持范数,所以 \( T(0)=0\),且上面两式右边相等,故 \( \|Tu-Tv\|=\|u-v\|\),即 \( T\) 是等距变换,。
如果 \( T\) 是等距变换,并且 \( T(0)=0\),那么上面两式左边相等,且 \( \|Tu\|=\|Tu-T0\|=\|u-0\|=\|u\|\),从而 \( \mathrm{Re}\,\langle Tu,Tv\rangle=\mathrm{Re}\,\langle u,v\rangle\)。
以下是两个反例,证明关系图中的两个单项箭头不可能是双向的。
反例1:设 \( f\) 是复数域上的变换,\( f(z)=\bar z\),那么因为 \( |\bar{z_1}-\bar{z_2}|=|z_1-z_2|\) 所以 \( f\) 是复向量空间中的等距变换,并且 \( f(0)=0\),但是 \( f\) 不是线性的,也不保持内积,但是保持内积的实部。
反例2:设 \( f\) 是实数域上的变换,\( f(x)=|x|\),那么 \( f\) 保持范数,但它不保持内积实部,也不是等距变换。
参考文献:
[1] 侯维民. 关于正交变换两种定义方式的探讨 [J]. 高等数学研究, 2005, 8(1): 44-45.
[2] [美] Peter.D.Lax. 线性代数及其应用 [M]. 傅莺莺,沈复兴,译. 北京:人民邮电出版社,2009.
7 极分解的另一种形式
一个线性变换 \( T\) 的极分解 \( T=S\sqrt{T^*T}\) 表明,\( T\) 的作用相当于先在某些方向上进行伸缩变换(半正定变换 \( \sqrt{T^*T}\) 的作用,根据谱定理),然后再进行等距变换 \( S\)。
那么,如果取 \( T^*\) 的极分解 \( T^*=S\sqrt{TT^*}\),则 \( T=\sqrt{TT^*}S^*\),则表明 \( T\) 也可以看作先做等距变换,然后再在某些方向上伸缩。
部分习题解答:
5 证明如果 \( \dim V\ge 2\),那么所有 \( V\) 上的正规算子的集合不是 \( \mathcal L(V)\) 的子空间。
证明:考察下面等式:
\( \begin{pmatrix}2&1\\ -1&2\end{pmatrix}+\begin{pmatrix}2&1\\ 1&2\end{pmatrix}=\begin{pmatrix}4&2\\ 0&4\end{pmatrix}\)
等式左边一个为正规算子,一个为自伴算子,它们的和不是正规的。
7 证明如果 \( T\in\mathcal L(V)\) 是正规算子,那么对所有正整数 k,有 \( \mathrm{null}\,T^k=\mathrm{null}\,T, \mathrm{range}\,T^k=\mathrm{range}\,T\)。
证明:当 k=1 时命题显然成立。假设当 k=m 时,命题成立,那么 \( \forall v\in \mathrm{null}\,T^{m+1}\),有 \( TT^mv=0\),即 \( T^mv\in\mathrm{null}\,T\) 又因 \( T^mv\in\mathrm{range}\,T\) 且 \( (\mathrm{null}\,T)^\perp=\mathrm{range}\,T\),那么 \( T^mv=0\),根据归纳假设,\( v\in\mathrm{null}\,T\)。可见 \( \mathrm{null}\,T^{m+1}\subset\mathrm{null}\,T\)。另一个方向的包含是显然的,所以 \( \mathrm{null}\,T^{m+1}=\mathrm{null}\,T\),
因为 \( T^k\) 也是正规的,所以 \( \mathrm{range}\,T^k=(\mathrm{null}\,T^k)^\perp\)\( =(\mathrm{null}\,T)^\perp=\mathrm{range}\,T\)。
14 设 \( T\in\mathcal L(V)\) 是自伴算子,\( \lambda\in\mathbf F, \epsilon>0\),证明如果存在向量 \( v\in V\) 满足 \( \|v\|=1\) 且 \( \|Tv-\lambda v\|<\epsilon\),那么 \( T\) 有特征值 \( \lambda’\) 满足 \( |\lambda-\lambda’|<\epsilon\)。
证明:根据自伴算子的谱定理,存在一组正交基底使得 \( T\) 的矩阵是对角矩阵 \( \mathrm{diag}\,(\lambda_1,\lambda_2\dots,\lambda_n)\),那么
\( \min_i |\lambda_i-\lambda|^2\le\sum_{i=1}^n|\lambda_i-\lambda|^2v_i^2=\|Tv-\lambda v\|^2<\epsilon^2\)
取 \( \lambda’\) 是与 \( \lambda\) 最接近的特征值即可。
18 证明如果 \( T\) 是 \( V\) 上的半正定算子,那么对任意正整数 k,\( T^k\) 也是半正定的。
证明:可以用谱定理。这里例举另一个证明。
当 k 为偶数时,有
\( \langle T^kv,v\rangle=\langle T^{\frac{k}{2}}v,T^{\frac{k}{2}}v\rangle\ge 0\)
当 k 为奇数时,有
\( \langle T^kv,v\rangle=\langle TT^{\frac{k-1}{2}}v,T^{\frac{k-1}{2}}v\rangle\ge 0\)
24 设 \( T\in\mathcal L(V)\),\( S\in\mathcal L(V)\) 是 V 上的线性等距变换, \( R\in\mathcal L(V)\) 是 V 上的半正定算子且 \( T=SR\),证明 \( R=\sqrt{T^*T}\)。
证明:因 \( R\) 是半正定算子,所以只需证 \( R^2=T^*T\)。
因 \( R\) 自伴且 \( S\) 是线性等距变换,所以 \( T^*T=RS^{-1}SR=R^2\)。
27 证明或给出反例:如果 \( T\in\mathcal L(V)\),那么 \( T^2\) 的奇异值是 \( T\) 的奇异值的平方。
证明:取 \( T(x,y)=(0,x)\),则 \( T^2=0\),但 \( \sqrt{T^*T}(x,y)=(x,0)\),所以 \( T^2\) 的奇异值都为零,不等于 \( T\) 的奇异值的平方 (1和0)。